
Labyrinthe parfait 
Labyrinthe imparfait |
Étude des labyrinthes Dans des trames de carrés Les labyrinthes peuvent être étudiés comme des objets mathématiques, c'est la modélisation mathématique de labyrinthe. Deux aspects importants de cette modélisation sont la génération automatique de labyrinthe et la résolution de labyrinthe. Ces deux surfaces ne sont topologiquement pas équivalentes. Cette différence, rapportée aux labyrinthes, conduit à une distinction en deux catégories : celle des labyrinthes dits "parfaits" où chaque cellule est reliée à toutes les autres et, ce, de manière unique. celle des labyrinthes dits "imparfaits" qui sont tous les labyrinthes qui ne sont pas parfaits (ils peuvent donc contenir des boucles, des îlots ou des cellules inaccessibles). |
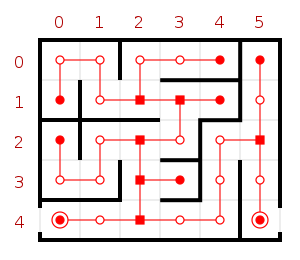
Un labyrinthe parfait et son DAG associé (en rouge). Les nœuds sont marqués selon qu'il s'agit d'entrées ou de sorties, d'intersections ou de cul-de-sac. | 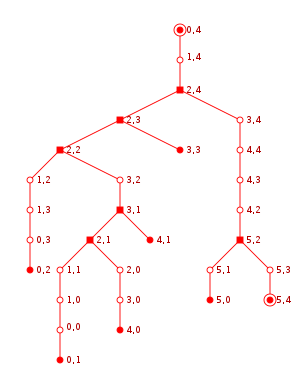
Représentation en arbre du labyrinthe [1]. |